Delve into the realm of composite figures and unravel the intricacies of calculating their areas. This comprehensive guide, “Area of Composite Figures Assignment,” serves as an authoritative resource, empowering you with the knowledge and techniques to tackle this fundamental concept with confidence.
From the basics of identifying composite shapes to the application of geometric formulas, this assignment equips you with a thorough understanding of area calculations. Prepare to embark on a journey of discovery, unlocking the secrets of composite figures and their real-world applications.
Types of Composite Figures: Area Of Composite Figures Assignment
Composite figures are geometric shapes formed by combining two or more basic shapes. They are commonly found in various fields, including architecture, design, and engineering.
Basic shapes used to create composite figures include rectangles, triangles, trapezoids, and circles. These basic shapes can be combined in different ways to form a wide range of composite figures, each with its unique properties and applications.
Examples of Composite Figures
- Rectangular prism:Formed by combining six rectangles, with two parallel faces being congruent.
- Triangular pyramid:Formed by combining four triangles, with one triangle serving as the base and the other three forming the sides.
- Trapezoidal prism:Formed by combining two trapezoids and four rectangles, with the trapezoids forming the bases.
- Circular cylinder:Formed by combining two circles and a rectangular strip, with the circles serving as the bases.
Methods for Calculating Area
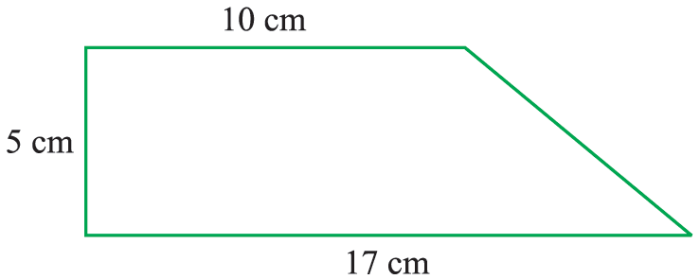
Calculating the area of composite figures requires understanding the formulas and techniques for determining the area of individual shapes that make up the composite figure. Here are some common methods for calculating area:
Formula for Calculating the Area of a Rectangle
The area of a rectangle is calculated by multiplying its length by its width. The formula is:
A = L x W
where:
- A is the area of the rectangle
- L is the length of the rectangle
- W is the width of the rectangle
Using the Pythagorean Theorem to Calculate the Area of a Triangle
The area of a triangle can be calculated using the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
The formula for calculating the area of a triangle is:
A = (1/2) x b x h
where:
- A is the area of the triangle
- b is the base of the triangle
- h is the height of the triangle
Formula for Calculating the Area of a Trapezoid, Area of composite figures assignment
The area of a trapezoid is calculated by multiplying the average of its two parallel sides by its height. The formula is:
A = (1/2) x (b1 + b2) x h
where:
- A is the area of the trapezoid
- b1 is the length of one parallel side
- b2 is the length of the other parallel side
- h is the height of the trapezoid
Formula for Calculating the Area of a Circle
The area of a circle is calculated by multiplying the square of its radius by pi (π), a mathematical constant approximately equal to 3. 14. The formula is:
A = πr²
where:
- A is the area of the circle
- r is the radius of the circle
Examples of Area Calculations
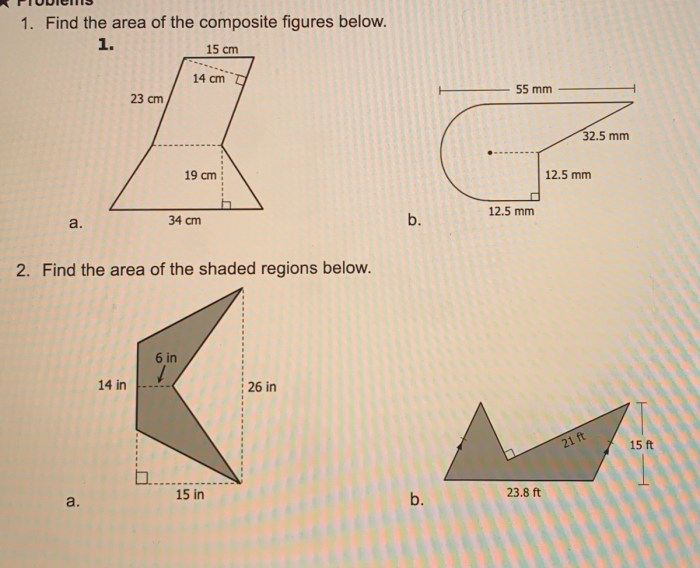
To illustrate the methods discussed earlier, let’s delve into specific examples of composite figures and demonstrate how to calculate their areas.
Rectangular and Triangular Combinations
Consider a composite figure consisting of a rectangle and a right triangle. The rectangle has a length of 10 cm and a width of 5 cm, while the triangle has a base of 6 cm and a height of 8 cm.
To calculate the area of this composite figure, we first calculate the areas of the individual shapes separately:
- Area of rectangle = Length × Width = 10 cm × 5 cm = 50 cm 2
- Area of triangle = 1/2 × Base × Height = 1/2 × 6 cm × 8 cm = 24 cm 2
Finally, we add the areas of the rectangle and triangle to get the total area of the composite figure:
Area of composite figure = Area of rectangle + Area of triangle = 50 cm 2+ 24 cm 2= 74 cm 2
Applications of Composite Figures
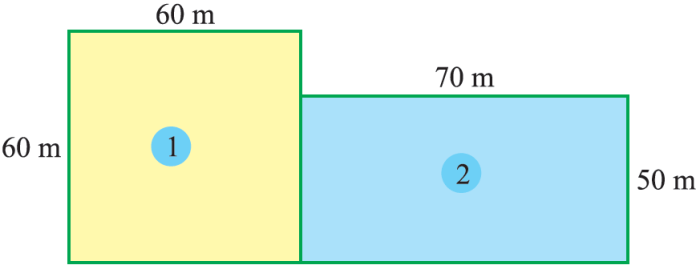
Composite figures are widely utilized in real-world applications, particularly in architecture and engineering. They enable the creation of complex structures with diverse shapes and functionalities.
In architecture, composite figures are employed to design buildings with intricate facades, curved roofs, and non-rectangular floor plans. For instance, the Burj Khalifa, the world’s tallest building, features a composite design that incorporates triangular and rectangular shapes to achieve its iconic silhouette.
Engineering
In engineering, composite figures are crucial for designing bridges, machines, and other structures that require specific shapes and load-bearing capacities. For example, suspension bridges employ composite figures such as parabolic curves to distribute the weight of the bridge deck evenly across the cables.
Machines
Composite figures are also used in the design of machines, such as gears, pulleys, and camshafts. The specific shapes of these components are designed to transmit motion, change direction, or regulate speed efficiently.
Q&A
What are the different types of composite figures?
Composite figures are formed by combining two or more basic shapes, such as rectangles, triangles, trapezoids, and circles.
How do I calculate the area of a composite figure?
To calculate the area of a composite figure, divide it into its individual shapes and calculate the area of each shape separately. Then, add the areas of the individual shapes to get the total area of the composite figure.
What are some real-world applications of composite figures?
Composite figures are used in a wide range of real-world applications, including architecture, engineering, and design. For example, buildings, bridges, and machines often incorporate composite figures in their construction.