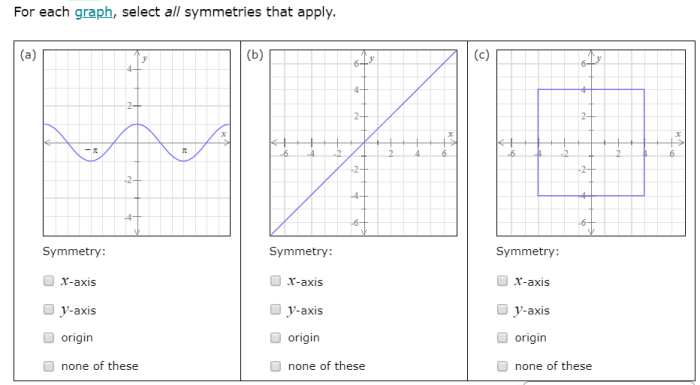
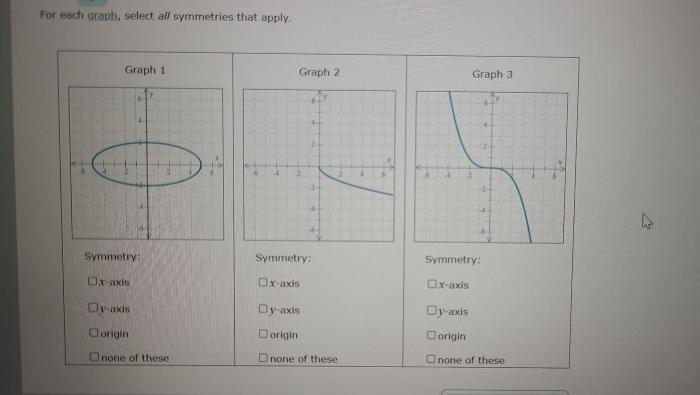
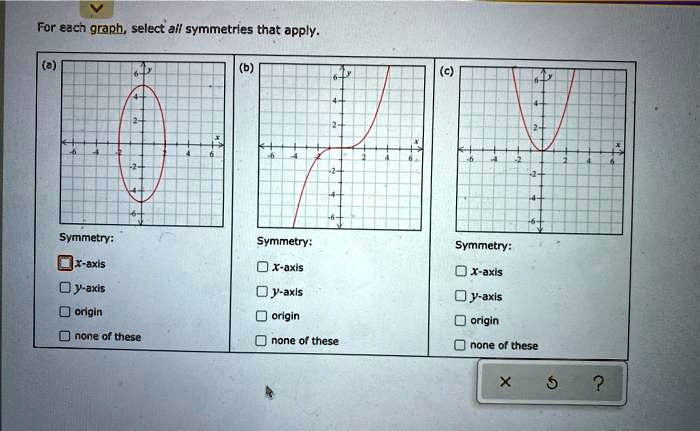
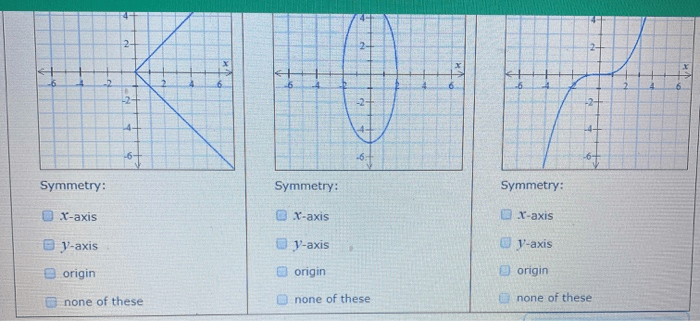
Symmetry, the balance and arrangement of elements in a pattern, is a fundamental concept found throughout mathematics, art, and nature. Select all symmetries that apply, and delve into the captivating world of symmetry, uncovering its diverse manifestations and practical applications.

From the intricate designs of ancient architecture to the harmonious patterns in nature, symmetry has captivated human imagination for centuries. This comprehensive guide explores the different types of symmetries, their significance in various fields, and their real-world applications.

Symmetry Types

Symmetry refers to the arrangement of elements in a way that creates a sense of balance and order. In mathematics and art, various types of symmetries exist, each with distinct characteristics.

The following table summarizes the different types of symmetries:

Type	Description	Example	Image
Line Symmetry	A figure is line-symmetric if it can be folded along a line (axis of symmetry) to produce two identical halves.	Rectangle, circle, human body	[Image of a rectangle folded along a line]
Rotational Symmetry	A figure has rotational symmetry if it can be rotated around a fixed point (center of rotation) by a certain angle to produce the same figure.	Circle, snowflake, flower	[Image of a snowflake rotating around its center]
Reflection Symmetry	A figure has reflection symmetry if it can be flipped over a line (axis of symmetry) to produce an identical mirror image.	Butterfly, heart, equilateral triangle	[Image of a butterfly with its wings folded]
Translation Symmetry	A figure has translation symmetry if it can be moved (translated) along a line without changing its shape or size.	Floor tiles, wallpaper patterns, crystals	[Image of floor tiles with a repeating pattern]

Symmetry in Art: Select All Symmetries That Apply

Symmetry plays a significant role in art and design. It creates a sense of balance, harmony, and aesthetic appeal.

The following table showcases different ways symmetry is used in art:

Type	Description	Example	Image
Bilateral Symmetry	An artwork is bilaterally symmetric if it can be divided into two identical halves by a vertical or horizontal line.	Mona Lisa by Leonardo da Vinci	[Image of the Mona Lisa]
Radial Symmetry	An artwork has radial symmetry if it can be divided into identical sectors by rotating it around a central point.	The Starry Night by Vincent van Gogh	[Image of The Starry Night]
Asymmetrical Symmetry	An artwork that does not exhibit any obvious symmetry but still creates a sense of balance and harmony.	Guernica by Pablo Picasso	[Image of Guernica]
Dynamic Symmetry	A type of symmetry that creates a sense of movement and energy in an artwork.	The Wave by Hokusai	[Image of The Wave]

Symmetry in Nature

Symmetry is prevalent in nature, from the microscopic to the macroscopic level.

• Bilateral Symmetry:Animals, insects, plants, and human bodies.
• Radial Symmetry:Flowers, starfish, jellyfish, and some sea creatures.
• Spherical Symmetry:Sun, moon, planets, and some crystals.
• Translational Symmetry:Honeycomb, crystal lattice, and some plant structures.
• Fractal Symmetry:Trees, ferns, and coastlines.

Symmetry in Mathematics

Symmetry plays a fundamental role in mathematics, particularly in geometry, algebra, and topology.

The following table illustrates the applications of symmetry in mathematics:

Field	Application	Example	Image
Geometry	Shape recognition, transformations, and proofs	Platonic solids, symmetry groups	[Image of Platonic solids]
Algebra	Group theory, equation solving, and polynomial factorization	Permutation groups, symmetric polynomials	[Image of a permutation group]
Topology	Classification of surfaces, knot theory, and differential geometry	Klein bottle, Möbius strip	[Image of a Klein bottle]
Analysis	Fourier analysis, harmonic functions, and differential equations	Symmetry breaking, conservation laws	[Image of a harmonic function]

Applications of Symmetry

The practical applications of symmetry extend beyond mathematics and art into various fields.

• Architecture:Buildings, bridges, and other structures.
• Engineering:Design of aircraft, cars, and machinery.
• Physics:Crystallography, particle physics, and quantum mechanics.
• Chemistry:Molecular structure and bonding.
• Biology:DNA structure, protein folding, and animal locomotion.

FAQ Summary

What is the difference between rotational and translational symmetry?

Rotational symmetry refers to the repetition of a pattern when rotated around a fixed point, while translational symmetry refers to the repetition of a pattern when moved in a specific direction.

Can symmetry be found in everyday objects?

Yes, symmetry is prevalent in everyday objects, such as the symmetrical shape of a snowflake, the bilateral symmetry of a butterfly, or the radial symmetry of a flower.