Triangle congruence by ASA and AAS practice plays a crucial role in geometry, providing a solid foundation for understanding triangle relationships and properties. In this comprehensive guide, we will delve into the Angle-Side-Angle (ASA) and Angle-Angle-Side (AAS) congruence theorems, exploring their applications and intricacies.
We will examine the conditions under which these theorems can be applied, illustrate their usage through practical examples, and provide step-by-step solutions to practice problems. By engaging in this practice, students will develop a deep understanding of triangle congruence, its significance in geometric proofs, and its relevance in various mathematical applications.
Triangle Congruence by ASA
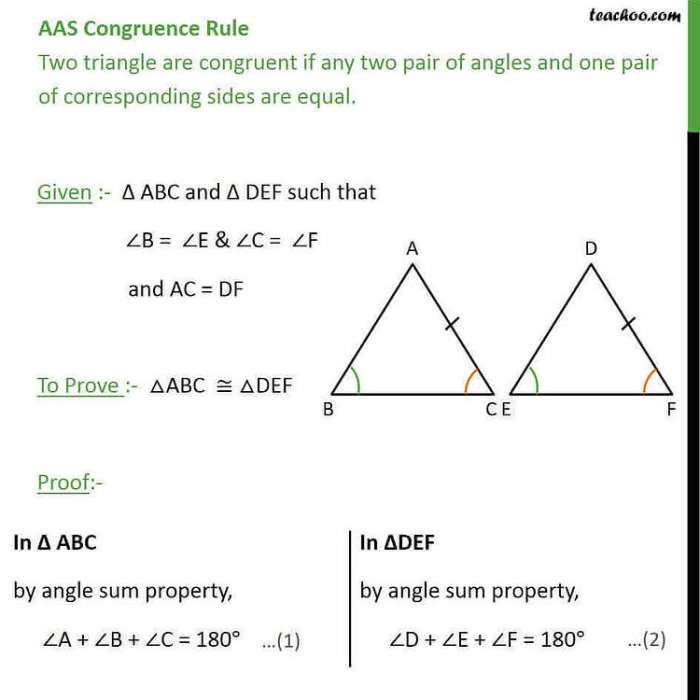
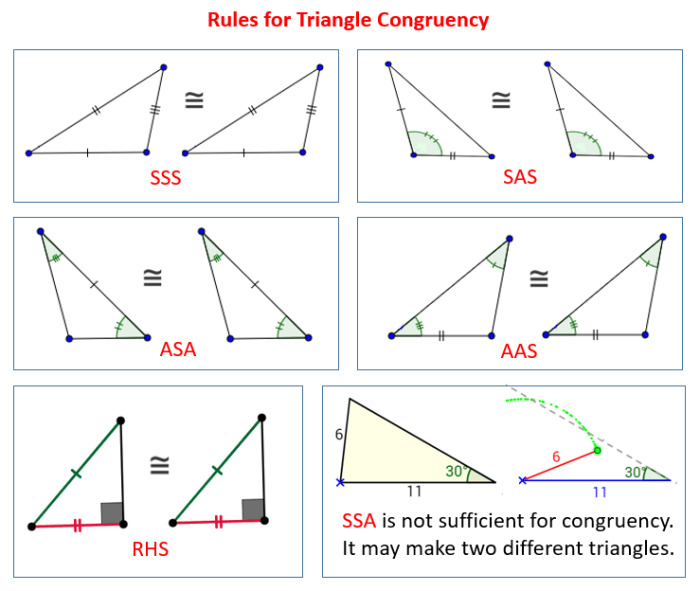
The Angle-Side-Angle (ASA) congruence theorem states that if two triangles have two pairs of congruent angles and the included sides are congruent, then the triangles are congruent.
In other words, if ΔABC and ΔDEF have ∠A ≅ ∠D, ∠B ≅ ∠E, and AB ≅ DE, then ΔABC ≅ ΔDEF.
Examples of Triangles that are Congruent by ASA, Triangle congruence by asa and aas practice
- Two equilateral triangles are congruent by ASA because they have three pairs of congruent angles and three pairs of congruent sides.
- Two isosceles triangles with congruent bases are congruent by ASA because they have two pairs of congruent angles and the included sides are congruent.
- Two right triangles with congruent hypotenuses are congruent by ASA because they have two pairs of congruent angles and the included sides are congruent.
Demonstrating Triangle Congruence Using the ASA Theorem
To prove that two triangles are congruent by ASA, we need to show that they have two pairs of congruent angles and the included sides are congruent. This can be done by using the following steps:
- Show that two pairs of angles are congruent.
- Show that the included sides are congruent.
- Use the ASA congruence theorem to conclude that the triangles are congruent.
Triangle Congruence by AAS
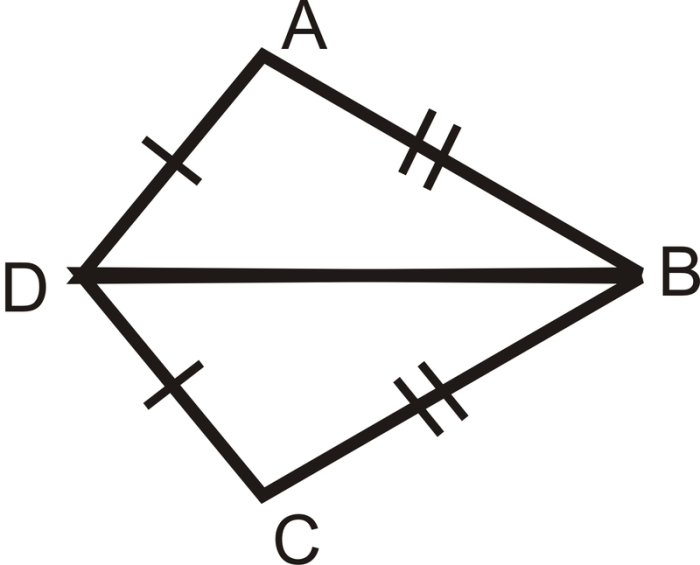
The Angle-Angle-Side (AAS) congruence theorem states that if two triangles have two pairs of congruent angles and a pair of congruent non-included sides, then the triangles are congruent.
In other words, if ΔABC and ΔDEF have ∠A ≅ ∠D, ∠B ≅ ∠E, and AC ≅ DF, then ΔABC ≅ ΔDEF.
Examples of Triangles that are Congruent by AAS
- Two right triangles with congruent legs are congruent by AAS because they have two pairs of congruent angles and a pair of congruent non-included sides.
- Two isosceles triangles with congruent bases are congruent by AAS because they have two pairs of congruent angles and a pair of congruent non-included sides.
- Two equilateral triangles are congruent by AAS because they have two pairs of congruent angles and a pair of congruent non-included sides.
Demonstrating Triangle Congruence Using the AAS Theorem
To prove that two triangles are congruent by AAS, we need to show that they have two pairs of congruent angles and a pair of congruent non-included sides. This can be done by using the following steps:
- Show that two pairs of angles are congruent.
- Show that a pair of non-included sides are congruent.
- Use the AAS congruence theorem to conclude that the triangles are congruent.
Comparing ASA and AAS
The ASA and AAS congruence theorems are both used to prove that two triangles are congruent. However, there are some key differences between the two theorems.
The ASA congruence theorem requires that two pairs of angles and the included sides are congruent. The AAS congruence theorem requires that two pairs of angles and a pair of non-included sides are congruent.
The ASA congruence theorem is more commonly used than the AAS congruence theorem because it is easier to apply. The AAS congruence theorem can only be used if one of the non-included sides is congruent.
Practice Problems
| Problem | Solution |
|---|---|
| Prove that ΔABC and ΔDEF are congruent by ASA. | Given: ∠A ≅ ∠D, ∠B ≅ ∠E, and AB ≅ DETo prove: ΔABC ≅ ΔDEFProof:
|
| Prove that ΔGHI and ΔJKL are congruent by AAS. | Given: ∠G ≅ ∠J, ∠H ≅ ∠K, and GH ≅ JKTo prove: ΔGHI ≅ ΔJKLProof:
|
FAQs: Triangle Congruence By Asa And Aas Practice
What is the Angle-Side-Angle (ASA) congruence theorem?
The ASA congruence theorem states that if two triangles have two angles and the included side congruent, then the triangles are congruent.
What is the Angle-Angle-Side (AAS) congruence theorem?
The AAS congruence theorem states that if two triangles have two angles and a non-included side congruent, then the triangles are congruent.
What are the conditions under which the ASA and AAS congruence theorems can be applied?
The ASA congruence theorem can be applied when two angles and the included side of one triangle are congruent to two angles and the included side of another triangle. The AAS congruence theorem can be applied when two angles and a non-included side of one triangle are congruent to two angles and a non-included side of another triangle.
What are the applications of triangle congruence by ASA and AAS?
Triangle congruence by ASA and AAS is used in various applications, including geometric proofs, construction, and design. It is also used in fields such as architecture, engineering, and surveying.