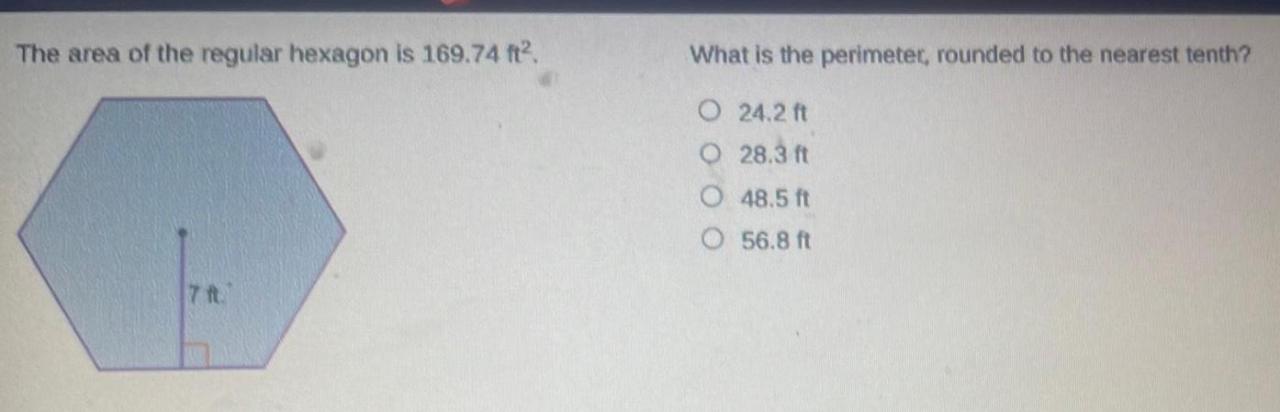
The area of the regular hexagon is 169.74 ft2 – The area of a regular hexagon with a side length of 169.74 ft2 presents a fascinating exploration into the realm of geometry. Regular hexagons, with their six equal sides and six equal angles, possess unique properties and applications that have captivated mathematicians, architects, and artists for centuries.

Join us as we delve into the intriguing world of regular hexagons, uncovering the secrets behind their area, perimeter, and captivating characteristics.

Our journey begins with a thorough examination of the formula used to calculate the area of a regular hexagon, exploring its derivation and significance. We will then investigate the relationship between the area and perimeter of a regular hexagon, unveiling the underlying mathematical connections that govern these geometric figures.

1. Definition of Regular Hexagon

A regular hexagon is a polygon with six equal sides and six equal interior angles. It is a two-dimensional shape that belongs to the family of regular polygons.

The interior angles of a regular hexagon measure 120 degrees each, and the sum of all interior angles is 720 degrees.

2. Area Formula for Regular Hexagon

The area of a regular hexagon is given by the formula:

A = (3√3/2)s^2

where:

• A is the area of the hexagon
• s is the length of one side of the hexagon

This formula is derived from the fact that a regular hexagon can be divided into six equilateral triangles, each with an area of (√3/4)s^2. The total area of the hexagon is then the sum of the areas of these triangles.

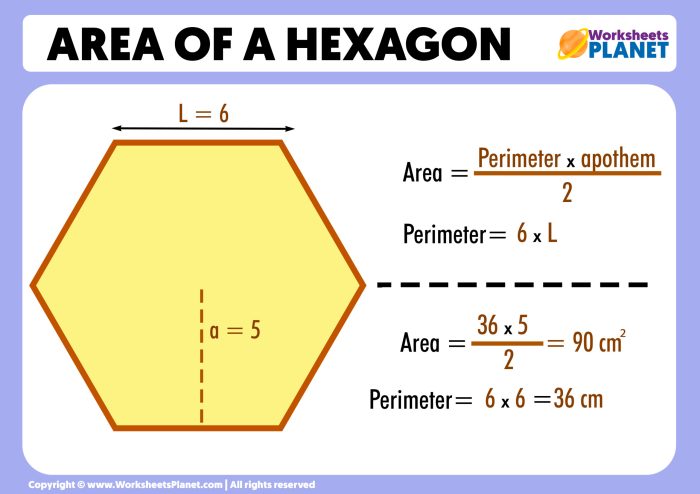
3. Perimeter of Regular Hexagon

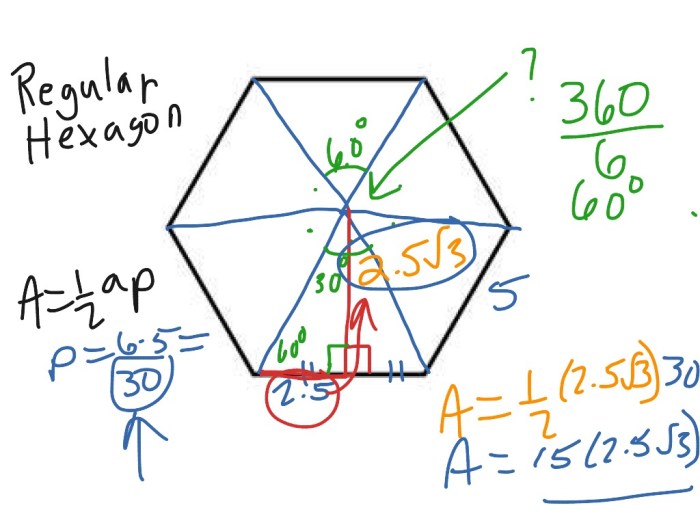
The perimeter of a regular hexagon is given by the formula:

P = 6s

where:

• P is the perimeter of the hexagon
• s is the length of one side of the hexagon

This formula is simply the sum of the lengths of all six sides of the hexagon.

4. Applications of Regular Hexagon

Regular hexagons are used in a variety of applications, including:

• Architecture:Regular hexagons are often used in the design of buildings and other structures because they are strong and stable.
• Engineering:Regular hexagons are used in the design of bridges, towers, and other structures that require strength and stability.
• Design:Regular hexagons are used in the design of furniture, fabrics, and other objects because they are aesthetically pleasing.

5. Inscribed and Circumscribed Circles

An inscribed circle is a circle that is tangent to all six sides of a regular hexagon. A circumscribed circle is a circle that passes through all six vertices of a regular hexagon.

The radius of the inscribed circle is given by:

r = (s/2)cot(π/6)

where:

• r is the radius of the inscribed circle
• s is the length of one side of the hexagon

The radius of the circumscribed circle is given by:

R = (s/2)csc(π/6)

where:

• R is the radius of the circumscribed circle
• s is the length of one side of the hexagon

6. Properties of Regular Hexagons

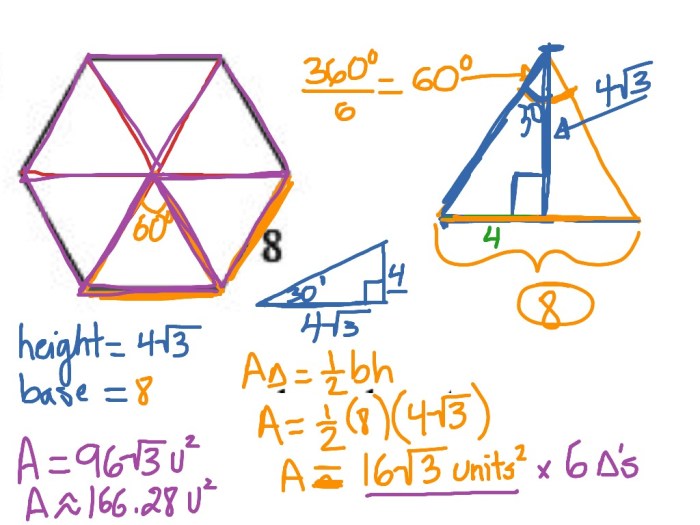
Regular hexagons have a number of interesting properties, including:

• Symmetry:Regular hexagons have six lines of symmetry.
• Congruence:All six sides and all six interior angles of a regular hexagon are congruent.
• Tessellation:Regular hexagons can be tessellated, or tiled, to fill a plane without any gaps or overlaps.

7. Honeycomb Structure: The Area Of The Regular Hexagon Is 169.74 Ft2

The honeycomb structure found in nature is composed of hexagonal cells. This structure is strong and lightweight, and it is able to withstand a lot of pressure.

The hexagonal shape of the cells is the optimal shape for creating a strong and stable structure. This is because the hexagonal shape distributes the pressure evenly throughout the structure.

8. Artistic and Cultural Significance

Regular hexagons have been used in art, architecture, and design for centuries.

Some famous examples of structures that incorporate regular hexagons include:

• The Great Mosque of Damascus
• The Taj Mahal
• The honeycomb structure of a beehive

Answers to Common Questions

What is the formula for calculating the area of a regular hexagon?

The area of a regular hexagon can be calculated using the formula: Area = (3√3 / 2) – s^2, where ‘s’ represents the length of one side of the hexagon.

How is the perimeter of a regular hexagon related to its area?

The perimeter of a regular hexagon is directly proportional to its area. As the area of the hexagon increases, its perimeter also increases.

What are some real-world applications of regular hexagons?

Regular hexagons are commonly used in architecture, engineering, and design due to their structural stability and aesthetic appeal. Examples include honeycomb structures, floor tiling, and architectural facades.