Segment lengths formed by chords secants and tangents – In the realm of geometry, the lengths of segments formed by chords, secants, and tangents play a pivotal role in shaping the properties of circles. This comprehensive exploration delves into the intricate relationships between these segments, unraveling their formulas, applications, and comparative characteristics.
From the fundamental concept of chords to the intriguing properties of tangents, this discourse provides a thorough understanding of these geometric elements, empowering readers with a deeper appreciation for the intricacies of circular geometry.
Segment Lengths Formed by Chords
A chord is a line segment that connects two points on a circle. The length of a chord is determined by the radius of the circle and the distance between the two points.
The formula for calculating the length of a chord is:
$$c = 2r\sin(\theta/2)$$
where:
- c is the length of the chord
- r is the radius of the circle
- θ is the central angle formed by the chord
Chords are used in a variety of applications, such as:
- Construction
- Navigation
- Engineering
Segment Lengths Formed by Secants
A secant is a line that intersects a circle at two points. The length of a secant is determined by the radius of the circle and the distance between the two points of intersection.
The formula for calculating the length of a secant is:
$$s = 2r\tan(\theta/2)$$
where:
- s is the length of the secant
- r is the radius of the circle
- θ is the central angle formed by the secant
Secants are used in a variety of applications, such as:
- Construction
- Navigation
- Engineering
Segment Lengths Formed by Tangents
A tangent is a line that intersects a circle at only one point. The length of a tangent is determined by the radius of the circle and the distance between the point of tangency and the center of the circle.
The formula for calculating the length of a tangent is:
$$t = r\sqrt2(1-\cos\theta)$$
where:
- t is the length of the tangent
- r is the radius of the circle
- θ is the central angle formed by the tangent
Tangents are used in a variety of applications, such as:
- Construction
- Navigation
- Engineering
Comparative Analysis of Segment Lengths: Segment Lengths Formed By Chords Secants And Tangents
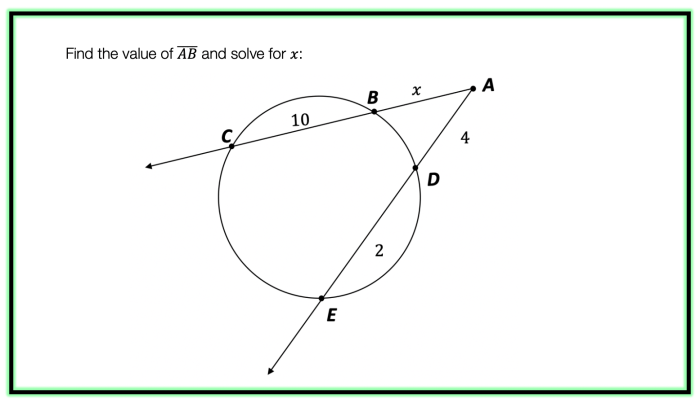
The lengths of chords, secants, and tangents can be compared using the following table:
| Segment Type | Formula | Length |
|---|---|---|
| Chord | $$c = 2r\sin(\theta/2)$$ | Less than the diameter |
| Secant | $$s = 2r\tan(\theta/2)$$ | Greater than the diameter |
| Tangent | $$t = r\sqrt2(1-\cos\theta)$$ | Equal to the radius |
The length of a chord is always less than the diameter of the circle, while the length of a secant is always greater than the diameter. The length of a tangent is always equal to the radius of the circle.
Applications in Geometry and Trigonometry
The concept of segment lengths formed by chords, secants, and tangents is used in a variety of applications in geometry and trigonometry.
In geometry, these concepts are used to:
- Construct circles and other geometric shapes
- Solve geometric problems
- Prove geometric theorems
In trigonometry, these concepts are used to:
- Define trigonometric functions
- Solve trigonometric equations
- Apply trigonometry to real-world problems
Quick FAQs
What is the formula for calculating the length of a chord?
The length of a chord can be calculated using the formula: Chord Length = 2√(r² – (d/2)²) where r is the radius of the circle and d is the distance between the chord and the center of the circle.
How are secants related to chords?
Secants are line segments that intersect a circle at two distinct points. The length of a secant is always greater than or equal to the length of the corresponding chord.
What is the significance of tangents in geometry?
Tangents are line segments that touch a circle at only one point. They are perpendicular to the radius drawn to the point of tangency and play a crucial role in various geometric constructions and applications.